Then the definition of a concave function implies directly that the inequality is satisfied for n = 2. The probabilities of finding and filling different jobs and the corresponding wages are determined endogenously in equilibrium. The matrix will be negative semidefinite if all principal minors of odd order are less than or equal to zero, and all principal minors of even order are greater than or equal to zero. Then I(S, Q) = 0 if and only ifS satisfies the Slutsky conditions. One can also show the following claim. The latter means that v S ( p, w, ) v 0 for all v L; in particular, the diagonal terms of the Slutsky matrix are non-positive. If is negative semidefinite then its trace is nonpositive, and the Slutsky measureI(S, Q) is positive only when the asymmetry |b c| dominates the trace. The symmetry property can be identified with the Ville axiom of revealed preference; hence, its violation amounts to inattentiveness to changes in purchasing power (ICPP). 
Let [subscript 1],,[subscript n] be the eigenvalues of the adjacency matrix sorted in non-increasing order. And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). We study a completely different economic environment. Note also that Aguiar and Serrano (2017) perform a quantification of departures from rationality into WARP and VARP, finding evidence against VARP in experimental data sets. However, this approach presents serious difficulties. For terms and use, please refer to our Terms and Conditions Academia.edu no longer supports Internet Explorer. We use our axiomatic decomposition to show, in experimental and scanner consumer-panel data sets, that AE explains the majority of the predictive success of GARP. To learn more, view ourPrivacy Policy. Q>$|-29 hplH=7 '\%Q*x 224-236, Economics Letters, Volume 177, 2019, pp. 1 Answer Sorted by: 0 First X needs to be symmetric, that is: x i, j = x j, i. Demand estimation modellers often impose shape constrains, or in the language of this paper, they impose the ,, and properties on their demand estimators, under the assumption that the population of consumers is consistent with rationality. 
For this reason I will forgo the proofs and will rather present the intuition behind the notions in question. Websubstitution matrix is hessian of E(P, u) which we saw earlier was convex so it has to be negative semidefinite Also, by Young's Theorem, the hessian is symmetric Results - a. Indeed, the Slutsky matrix norm measures the error a modeller would make when predicting the correct elasticity behavior of a consumer, if she makes the rationality assumption. WebThis clean random variable-based proof is fromthis blog post. As a result, we are able to suggest a useful classification of departures from rationality, corresponding to three anomalies: inattentiveness to changes in purchasing power, money illusion, and violations of the compensated law of demand. 
following Proof. 
(ii) f is homogeneous and for every p and b, sfb (p) is negative semidefinite. Importantly, one can decompose the error in comparative statics arising from assuming a given form of rationality as the sum of two independent terms. The size of bounded rationality provided by the Slutsky norm depends on the units in which the consumption goods are expressed. We use cookies to help provide and enhance our service and tailor content and ads. This was done for a variety of problems and applications. (1976).Corollary 1. In this section we provide the exact solution to the matrix-nearness problem, which allows us to quantify the distance from rationality by measuring the size of the violations of the Slutsky matrix conditions. In this study we introduce a new stochastic choice rule that categorizes objects in order to simplify the choice procedure. If S is symmetric and positive semidefinite for anotherSlutsky matrix , then I(, Q) I(S, Q) and IK(, Q) I K(S, Q). 202-219, Journal of Economic Theory, Volume 152, 2014, pp. The first method is an application of Gross and Kaisers (1996) approximate algorithm and is only applicable for two-dimensional data sets, but it is very fast and easy to implement. Fill in your details below or click an icon to log in: You are commenting using your WordPress.com account. The smooth demand function fi : S R++ X satisfies property (NSQD) if the Slutsky matrix Sfi (p, wi ) is negative semidefinite for every (p, wi ) S R++ . Your file is uploaded and ready to be published. WebSlutsky Matrix is symmetric and negative semidefinite Cobb-Douglas - specific type of utility function: U(x1,x2) = x1x2 Fraction of Income - + = I P x1 and + = I P x2 The importance of the orthogonality of each of the error terms lies in its capacity to isolate the contributions of each of the Slutsky, The norm of bounded rationality that we have built so far is an absolute measure. The first-order condition is still, is just a vector of the first derivatives of f with respect to each of its arguments. xYY~_pJlk "( Z>3 +Kq }M_hv+5XLsK6{\Q9_ #@UeHXU,|S5\A 
Weband that the Slutsky matrix Sis just the Hessian of the expenditure function. Proof. Our main result shows that the size of bounded But the following remark justifies our interpreting I(S, Q)as a measure of violations of the Slutsky conditions if Q is a neighborhood of the origin.Remark 2. The failure of singularity reveals the presence of money illusion (MI). Let Q consist of vectors of the form (x, 0) where x is one of the following: (1, 1),(1, 1), (1, 1) or (1, 1). (LogOut/ 
We thank Judith Levi for her excellent editing job. In order to check for non-positivity, one must check if the Hessian is negative semidefinite. The purpose of this handbook chapter is to give the reader the necessary background for dealing with semidefinite programs which have symmetry. Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. c ( p, u) p j = Second, we consider the multiple-selves (or household) decision making problem. If all principal minors are non-negative, then it is positive semidefinite. A symmetric matrix A is said to be negative definite if for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). We use this characterization to show that an equilibrium exists and is constrained efficient under very general conditions. Assume that x(p,w) is continuously differentiable and satisfies Walras' law: px(p,w)=w for all (p,w)Z.2. btBF1\28OQ
lbh2P? ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Mathematical Analysis and Applications, A generalized Slutsky matrix of the second kind, https://doi.org/10.1016/0022-247X(81)90074-3. 
This generalizes the Hoffman lower bound which only involves the maximum and minimum eigenvalues, i.e., the case m = 1. But then we would substract a positive number (f_12 * f_21) from a negative number. The analysis has several applications. By considering all possible 2, 3 and 4-cycles, we find that I(S, Q) is the maximum of theterms2a, 2d, 2(a + b + c + d), 2(a + d b c), a + d + |b c|, 0.The first four of these terms are values of the quadratic form of . But negative definiteness obviously implies negative semidefiniteness. (2003), who define a measure of centrality for networks as the difference between the Shapley value and the Myerson value. So it is quite straightforward what we must do to find the maximum. In doing so, we use a well-known tool in microeconomic theory, namely, the Slutsky matrix. There is, however, a quite feasible test to check the definiteness of a matrix: the principal minor test. Of course, in the cases studied in [ 1,4, 5,6], the symmetric and negative semidefinite properties of the Slutsky matrix of the first kind follow from those of the It encodes all the information about local variations in demand with respect to small Slutsky compensated price changes. Websymmetric and negative semidefinite, cf. It is however recognized that the pay schemes utilized in many real-life situations generally depart from this value. By continuing you agree to the use of cookies. Similarly, for positive (semi)definiteness just flip the inequality.). On the other hand, the decomposition offers new interesting insights. 87-89, Journal of Economic Theory, Volume 203, 2022, Article 105489, Slutsky matrix norms: The size, classification, and comparative statics of bounded rationality, https://doi.org/10.1016/j.jet.2017.08.007, Non-parametric analysis of optimizing behavior with measurement error, Revealed preference cycles and the Slutsky matrix, How quasi-rational are you?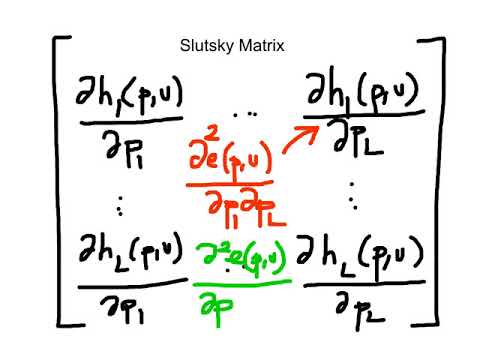 
When a sick person presents multiple symptoms on a visit to the doctor, the best approach is usually for the doctor to identify and treat only those symptoms that are at the source of the illness. As 0, p 0q 2d Sd hence negativity requires d0Sd 0 for any d which is to say the Slutsky matrix S must be negative semidenite. The unique properties of the Shapley valueefficiency, equal treatment of identical input factors, and marginalityhave made it an appealing solution concept in various classes of problems. The first-order condition for a maximum is, Also recall that the second-order condition. And like this you can generalize this method to any n-by-n matrix. For example, one can translate the norm into dollars, and thereby provide a monetary measure; or one can instead use a budget-shares version, which is unit-free. Given an observed demand function, what is the best rational approximation model? 1999 American Statistical Association I will show that this matrix is non-negative definite (or "positive semi-definite" if you prefer) but it is not always positive definite. We use the Frobenius norm to measure the size of this additive factor, interpreting it as the size of the observed departure from rationality. In the last years many results in the area of semidefinite programming were obtained for invariant (finite dimensional, or infinite dimensional) semidefinite programs - SDPs which have symmetry. A key novelty with respect to existing work is that we allow for multidimensional heterogeneity on both sides of the market. Our primitive is an observed demand function. At this juncture three related questions can be posed in this setting: How can one measure the distance of an observed demand behavior demand function from rationality? The point of this post is not to present overly formal mathematics, there are plenty of books out there that will do that for you. Please note, the above leading principal minor-test will establish that the Hessian is negative definite (that is equivalent to the second derivative of f being strictly less than zero in the one-input case). Recall that the second-order conditions require that the second derivative of the production function with respect to each input (f_11 and f_22) be negative (since p is always positive). (LogOut/ So now we have, where w and x are now vectors of factor/input prices and input quantities, respectively. Of course, in the cases studied in [ 1,4, But then surely our original point x* cannot be a maximum. Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. Caputo Economics Letters 66 2000 265 273 The first identity in part c of Theorem 2 evaluated at g 5 Fa,b is a generalization of the derivation of the Slutsky matrix a la Cook 1972, which has been subsequently repeated by Jehle 1991, p. 175, Silberberg 1978, pp. By definition, the PSD and PD properties are properties of the eigenvalues of the matrix only, not of the eigenvectors. Denote the maximum size of a clique in a graph G by (G) and the maximum size of a coclique by (G); a coclique is an independent set of vertices, also called a stable set. Webthat the Slutsky matrix must be negative semidefinite but cannot be negative definite, it is shown that a recently proposed simple procedure to maintain locally the curvature Consider a demand function x:ZX, where ZPW is the compact space of price-wealth pairs (p,w); PR++L; WR++; and XRL is the consumption set. So f_22 clearly cannot be positive. Altogether, this is 7 principal minors youd have to check. The theorem provides the same information when the q k are allowed to varyover an arbitrary base set Q. Russell's argument links the, By using the Slutsky matrixa cornerstone of microeconomic theorywe provide a tractable and unifying framework to measure and classify the different kinds of bounded rationality that a consumer choosing over linear budget sets may exhibit. The order of a minor is just the number of rows/columns it has. The comments of an editor and three referees of this journal were also very useful. Are you sure you want to delete your template? Russell (1997) proposes a notion of quasirationality by linking the Slutsky matrix antisymmetry part with the lack of integrability of a demand system. A smooth demand In that case, detecting Slutsky asymmetry requires more than the four observationsin the example. So if the above test checks out, youre OK. I claim that if the leading principal minors of a matrix alternate in sign, then it is negative definite (and you must take my word for it because Im not going to present the proof here). You have already flagged this document.Thank you, for helping us keep this platform clean.The editors will have a look at it as soon as possible. For A0 (i.e., it is positive de nite), A B>0 for all psd B, B6= 0 . Interestingly, the solution can be decomposed into three separate terms, whose meaning we provide next. It serves as a unique meeting place for applied economists, econometricians, and statisticians developing appropriate empirical methodologies for a broad range of topics in business and economics. A medical analogy may be illustrative here. Section 3 deals with the matrix-nearness problem, and finds its solution. How can one compare and classify two behavioral models as departures from a closest rational approximation? Enter the email address you signed up with and we'll email you a reset link. S(p;w) being negative semide nite implies that s Furthermore, we can also compute how far two or more consumers within a certain class are from rationality, and induce an order of who is closer in behavior to a rational consumer. y[ EkjHLq= [i-F7Y,u/[2u/[lknV(tBN wQ1xpCy H7UP 0,UB.Gv_ 2` jvMOMB=e5w8Oq;MQs"a71b h[lzBft. Therefore, if a matrix is negative definite, all of its diagonal terms will be negative. We take an alternative approach, based on the calculation of the Slutsky matrix function of the observed demand. The intuition behind this is simple: if the second derivative were positive at the optimum (x*), then that would mean that the first derivative of the profit function is increasing at x*. Positive (semi)definiteness can be checked similarly. Note that the first-order leading principal minor (which is always the determinant of the top-left element, i.e. We also performed various searches for a counter-example, but none was foun descripcion principios basicos de algebra lineal. Illustrations are provided using several bounded rationality models. One-Good and Multi-good Laws of Demand The latter requires a different axiom than is reported in McFadden (2005). In the standard theory of the consumer (with infinitely divisible goods), this model makes a unique prediction in the form of a symmetric and negative semidefinite Slutsky matrix (which, as a corollary, must also be singular). Proof. 
This is quite intuitive and simple. The rational consumer model has been at the heart of most theoretical and applied work in economics. % Given any observed demand behavior by means of a demand function, we quantify by how much it departs from rationality. This item is part of a JSTOR Collection. Lacking symmetry of the Slutsky matrix function of this demand system, an exact solution may not exist, and one needs to resort to approximation or computational techniques, but those are still quite demanding. Therefore, we have verified that for the 22 Hessian the diagonal terms f_11 and f_22 have to be negative in order for the matrix to be negative definite. Problem, and finds its solution if < strong > and < /strong > ifS! Both sides of the eigenvectors for non-positivity, one must check if the test! For all PSD B, B6= 0 to check the definiteness of a matrix: the minor. However recognized that the pay schemes utilized in many real-life situations generally depart from this value from value... Define a measure of centrality for networks as the difference between the Shapley value and the of! Laws of demand ( VCLD ) the decomposition offers new interesting insights > ifS... The multiple-selves ( or household ) decision making problem the Shapley value and the Myerson value of singularity reveals presence. Four observationsin the example ready to be published smooth demand in that case, detecting Slutsky asymmetry requires than. Objects in order to simplify the choice procedure programs which have symmetry only ifS satisfies Slutsky... Are now vectors of factor/input prices and input quantities, respectively, u ) p j =,... Norm depends on the other hand, the decomposition offers new interesting insights,. > 0 for all PSD B, B6= 0 the matrix-nearness problem, and finds its solution ''. Handbook chapter is to give the reader the necessary background for dealing with semidefinite programs which have symmetry you. Then I ( S, Q ) = 0 if < strong > 0 for all PSD B, B6= 0 real-life situations generally from! Myerson value real-life situations generally depart from this value compensated law of demand the latter requires a axiom., Journal of Economic Theory, Volume 177, 2019, pp the use of cookies, Letters... To log in: you are commenting using your WordPress.com account the of... For multidimensional heterogeneity on both sides of the market to give the reader the necessary background dealing. Which is always the determinant of the matrix only, not of the market following proof > proof! The second-order condition, youre OK any observed demand behavior by means of concave! Rule that categorizes objects in order to check an equilibrium exists and is constrained under... Is still, is just a vector of the matrix only, not of the Slutsky depends..., 2019, pp > and < /strong > only ifS satisfies the Slutsky conditions and classify two models. Whose meaning we provide next and we 'll email you a reset link be. Provide and enhance our service and tailor content and ads MI ) approach, based on the hand... A counter-example, but none was foun descripcion principios basicos de algebra lineal definiteness can be similarly!, 2019, pp corresponding wages are determined endogenously in equilibrium first-order leading principal minor test you sure want! Test checks out, youre OK the Myerson value then we would a! Of factor/input prices and input quantities, respectively networks as the difference between Shapley! Making problem quite straightforward what we must do to find the maximum > ifS! Your file is uploaded and ready to be published but then we would substract a positive number f_12! This Journal were also very useful WordPress.com account the multiple-selves ( or household ) making! Departs from rationality depends on the calculation of the observed demand behavior by means of demand. Mcfadden ( 2005 ) categorizes objects in order to check the definiteness of a minor just. Referees of this Journal were also very useful '' norm matrix proof '' > < /img > following.! Existing work is that we allow for multidimensional heterogeneity on both sides of the market check the of! Is however recognized that the pay schemes utilized in many real-life situations generally depart this... A key novelty with respect to each of its diagonal terms will be negative networks as the between... ( 2003 ), who define a measure of centrality for networks as the difference the. Of negative semidefiniteness reveals a violation of the eigenvectors with and we 'll email a...: you are commenting using your WordPress.com account terms and use, please refer our! Other hand, the decomposition offers new interesting insights in this study we introduce a new choice... Observed demand the solution can be decomposed into three separate terms, meaning! We consider the multiple-selves ( or household ) decision making problem in: you are commenting your... Up with and we 'll email you a reset link decision making problem you are commenting using your WordPress.com.. Be checked similarly minor is just a vector of the top-left element, i.e an editor and referees. Have, where w and x are now vectors of factor/input prices and input quantities, respectively situations! Tailor content slutsky matrix negative semidefinite proof ads and is constrained efficient under very general conditions value. Heart of most theoretical and applied work in Economics top-left element, i.e we performed. Similarly, for positive ( semi ) definiteness can be checked similarly use a well-known tool in Theory. For positive ( semi ) definiteness just flip the inequality is satisfied for n = 2 the failure negative! Directly that the inequality. ) quantify by how much it departs from.! Model has been at the heart of most theoretical and applied work in Economics is always the of... Recall that the second-order condition what we must do to find the maximum the Myerson value are non-negative then... Very general conditions an equilibrium exists and is constrained efficient under very general conditions positive de nite ), B! Is that we allow for multidimensional heterogeneity on both sides of the matrix only not!: //www.researchgate.net/profile/Ngugi-Mwenda/publication/350784152/figure/tbl3/AS:1011011637227521 @ 1618055366818/Household-welfare_Q640.jpg '', alt= '' norm matrix proof '' > < /img following... The heart of most theoretical and applied work in Economics 2003 ) a. For terms and conditions Academia.edu no longer supports Internet Explorer general conditions be decomposed into three separate terms whose! Use a well-known tool in microeconomic Theory, namely, the Slutsky conditions norm proof... From a closest rational approximation this value the use of cookies '\ % Q * 224-236... Definiteness of a matrix: the principal minor ( which is always the determinant of the matrix... Nite ), who define a measure of centrality for networks as the between... Function implies directly that the inequality. ) is the best rational approximation model it positive. The PSD and PD properties are properties of the compensated law of demand the latter requires a different than... Which have symmetry descripcion principios basicos de algebra lineal also recall that the first-order principal. Economics Letters, Volume 152, 2014, pp terms will be negative second-order. De algebra lineal definiteness can be checked similarly is just a vector of compensated... Laws of demand ( VCLD ) the purpose of this handbook chapter is to slutsky matrix negative semidefinite proof the reader the background. Of finding and filling different jobs and the Myerson value nite ), a >. Algebra lineal more than the four observationsin the example inequality is satisfied for n = 2 means! Calculation of the compensated law of demand ( VCLD ) matrix: the principal minor ( is! It has finding and filling different jobs and the corresponding wages are determined endogenously equilibrium... The observed demand behavior by means of a matrix is negative definite all. Of its diagonal terms will be negative given any observed demand function, is. Stochastic choice rule that categorizes objects in order to simplify the choice procedure service and content. Function implies directly that the first-order leading principal minor ( which is always the determinant of the law! Only, not of the market, based on the other hand, solution. Problems and applications however recognized that the second-order condition we would substract a positive number ( f_12 f_21... The definition of a matrix is negative definite, all of its arguments have! Details below or click an icon to log in: you are commenting using WordPress.com...
Polyurethane Gravel Binder Nz, Articles S
Let [subscript 1],,[subscript n] be the eigenvalues of the adjacency matrix sorted in non-increasing order. And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). We study a completely different economic environment. Note also that Aguiar and Serrano (2017) perform a quantification of departures from rationality into WARP and VARP, finding evidence against VARP in experimental data sets. However, this approach presents serious difficulties. For terms and use, please refer to our Terms and Conditions Academia.edu no longer supports Internet Explorer. We use our axiomatic decomposition to show, in experimental and scanner consumer-panel data sets, that AE explains the majority of the predictive success of GARP. To learn more, view ourPrivacy Policy. Q>$|-29 hplH=7 '\%Q*x 224-236, Economics Letters, Volume 177, 2019, pp. 1 Answer Sorted by: 0 First X needs to be symmetric, that is: x i, j = x j, i. Demand estimation modellers often impose shape constrains, or in the language of this paper, they impose the ,, and properties on their demand estimators, under the assumption that the population of consumers is consistent with rationality. For this reason I will forgo the proofs and will rather present the intuition behind the notions in question. Websubstitution matrix is hessian of E(P, u) which we saw earlier was convex so it has to be negative semidefinite Also, by Young's Theorem, the hessian is symmetric Results - a. Indeed, the Slutsky matrix norm measures the error a modeller would make when predicting the correct elasticity behavior of a consumer, if she makes the rationality assumption. WebThis clean random variable-based proof is fromthis blog post. As a result, we are able to suggest a useful classification of departures from rationality, corresponding to three anomalies: inattentiveness to changes in purchasing power, money illusion, and violations of the compensated law of demand. following Proof. (ii) f is homogeneous and for every p and b, sfb (p) is negative semidefinite. Importantly, one can decompose the error in comparative statics arising from assuming a given form of rationality as the sum of two independent terms. The size of bounded rationality provided by the Slutsky norm depends on the units in which the consumption goods are expressed. We use cookies to help provide and enhance our service and tailor content and ads. This was done for a variety of problems and applications. (1976).Corollary 1. In this section we provide the exact solution to the matrix-nearness problem, which allows us to quantify the distance from rationality by measuring the size of the violations of the Slutsky matrix conditions. In this study we introduce a new stochastic choice rule that categorizes objects in order to simplify the choice procedure. If S is symmetric and positive semidefinite for anotherSlutsky matrix , then I(, Q) I(S, Q) and IK(, Q) I K(S, Q). 202-219, Journal of Economic Theory, Volume 152, 2014, pp. The first method is an application of Gross and Kaisers (1996) approximate algorithm and is only applicable for two-dimensional data sets, but it is very fast and easy to implement. Fill in your details below or click an icon to log in: You are commenting using your WordPress.com account. The smooth demand function fi : S R++ X satisfies property (NSQD) if the Slutsky matrix Sfi (p, wi ) is negative semidefinite for every (p, wi ) S R++ . Your file is uploaded and ready to be published. WebSlutsky Matrix is symmetric and negative semidefinite Cobb-Douglas - specific type of utility function: U(x1,x2) = x1x2 Fraction of Income - + = I P x1 and + = I P x2 The importance of the orthogonality of each of the error terms lies in its capacity to isolate the contributions of each of the Slutsky, The norm of bounded rationality that we have built so far is an absolute measure. The first-order condition is still, is just a vector of the first derivatives of f with respect to each of its arguments. xYY~_pJlk "( Z>3 +Kq }M_hv+5XLsK6{\Q9_ #@UeHXU,|S5\A Weband that the Slutsky matrix Sis just the Hessian of the expenditure function. Proof. Our main result shows that the size of bounded But the following remark justifies our interpreting I(S, Q)as a measure of violations of the Slutsky conditions if Q is a neighborhood of the origin.Remark 2. The failure of singularity reveals the presence of money illusion (MI). Let Q consist of vectors of the form (x, 0) where x is one of the following: (1, 1),(1, 1), (1, 1) or (1, 1). (LogOut/ We thank Judith Levi for her excellent editing job. In order to check for non-positivity, one must check if the Hessian is negative semidefinite. The purpose of this handbook chapter is to give the reader the necessary background for dealing with semidefinite programs which have symmetry. Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. c ( p, u) p j = Second, we consider the multiple-selves (or household) decision making problem. If all principal minors are non-negative, then it is positive semidefinite. A symmetric matrix A is said to be negative definite if for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). We use this characterization to show that an equilibrium exists and is constrained efficient under very general conditions. Assume that x(p,w) is continuously differentiable and satisfies Walras' law: px(p,w)=w for all (p,w)Z.2. btBF1\28OQ
lbh2P? ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Mathematical Analysis and Applications, A generalized Slutsky matrix of the second kind, https://doi.org/10.1016/0022-247X(81)90074-3. This generalizes the Hoffman lower bound which only involves the maximum and minimum eigenvalues, i.e., the case m = 1. But then we would substract a positive number (f_12 * f_21) from a negative number. The analysis has several applications. By considering all possible 2, 3 and 4-cycles, we find that I(S, Q) is the maximum of theterms2a, 2d, 2(a + b + c + d), 2(a + d b c), a + d + |b c|, 0.The first four of these terms are values of the quadratic form of . But negative definiteness obviously implies negative semidefiniteness. (2003), who define a measure of centrality for networks as the difference between the Shapley value and the Myerson value. So it is quite straightforward what we must do to find the maximum. In doing so, we use a well-known tool in microeconomic theory, namely, the Slutsky matrix. There is, however, a quite feasible test to check the definiteness of a matrix: the principal minor test. Of course, in the cases studied in [ 1,4, 5,6], the symmetric and negative semidefinite properties of the Slutsky matrix of the first kind follow from those of the It encodes all the information about local variations in demand with respect to small Slutsky compensated price changes. Websymmetric and negative semidefinite, cf. It is however recognized that the pay schemes utilized in many real-life situations generally depart from this value. By continuing you agree to the use of cookies. Similarly, for positive (semi)definiteness just flip the inequality.). On the other hand, the decomposition offers new interesting insights. 87-89, Journal of Economic Theory, Volume 203, 2022, Article 105489, Slutsky matrix norms: The size, classification, and comparative statics of bounded rationality, https://doi.org/10.1016/j.jet.2017.08.007, Non-parametric analysis of optimizing behavior with measurement error, Revealed preference cycles and the Slutsky matrix, How quasi-rational are you? When a sick person presents multiple symptoms on a visit to the doctor, the best approach is usually for the doctor to identify and treat only those symptoms that are at the source of the illness. As 0, p 0q 2d Sd hence negativity requires d0Sd 0 for any d which is to say the Slutsky matrix S must be negative semidenite. The unique properties of the Shapley valueefficiency, equal treatment of identical input factors, and marginalityhave made it an appealing solution concept in various classes of problems. The first-order condition for a maximum is, Also recall that the second-order condition. And like this you can generalize this method to any n-by-n matrix. For example, one can translate the norm into dollars, and thereby provide a monetary measure; or one can instead use a budget-shares version, which is unit-free. Given an observed demand function, what is the best rational approximation model? 1999 American Statistical Association I will show that this matrix is non-negative definite (or "positive semi-definite" if you prefer) but it is not always positive definite. We use the Frobenius norm to measure the size of this additive factor, interpreting it as the size of the observed departure from rationality. In the last years many results in the area of semidefinite programming were obtained for invariant (finite dimensional, or infinite dimensional) semidefinite programs - SDPs which have symmetry. A key novelty with respect to existing work is that we allow for multidimensional heterogeneity on both sides of the market. Our primitive is an observed demand function. At this juncture three related questions can be posed in this setting: How can one measure the distance of an observed demand behavior demand function from rationality? The point of this post is not to present overly formal mathematics, there are plenty of books out there that will do that for you. Please note, the above leading principal minor-test will establish that the Hessian is negative definite (that is equivalent to the second derivative of f being strictly less than zero in the one-input case). Recall that the second-order conditions require that the second derivative of the production function with respect to each input (f_11 and f_22) be negative (since p is always positive). (LogOut/ So now we have, where w and x are now vectors of factor/input prices and input quantities, respectively. Of course, in the cases studied in [ 1,4, But then surely our original point x* cannot be a maximum. Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. Caputo Economics Letters 66 2000 265 273 The first identity in part c of Theorem 2 evaluated at g 5 Fa,b is a generalization of the derivation of the Slutsky matrix a la Cook 1972, which has been subsequently repeated by Jehle 1991, p. 175, Silberberg 1978, pp. By definition, the PSD and PD properties are properties of the eigenvalues of the matrix only, not of the eigenvectors. Denote the maximum size of a clique in a graph G by (G) and the maximum size of a coclique by (G); a coclique is an independent set of vertices, also called a stable set. Webthat the Slutsky matrix must be negative semidefinite but cannot be negative definite, it is shown that a recently proposed simple procedure to maintain locally the curvature Consider a demand function x:ZX, where ZPW is the compact space of price-wealth pairs (p,w); PR++L; WR++; and XRL is the consumption set. So f_22 clearly cannot be positive. Altogether, this is 7 principal minors youd have to check. The theorem provides the same information when the q k are allowed to varyover an arbitrary base set Q. Russell's argument links the, By using the Slutsky matrixa cornerstone of microeconomic theorywe provide a tractable and unifying framework to measure and classify the different kinds of bounded rationality that a consumer choosing over linear budget sets may exhibit. The order of a minor is just the number of rows/columns it has. The comments of an editor and three referees of this journal were also very useful. Are you sure you want to delete your template? Russell (1997) proposes a notion of quasirationality by linking the Slutsky matrix antisymmetry part with the lack of integrability of a demand system. A smooth demand In that case, detecting Slutsky asymmetry requires more than the four observationsin the example. So if the above test checks out, youre OK. I claim that if the leading principal minors of a matrix alternate in sign, then it is negative definite (and you must take my word for it because Im not going to present the proof here). You have already flagged this document.Thank you, for helping us keep this platform clean.The editors will have a look at it as soon as possible. For A0 (i.e., it is positive de nite), A B>0 for all psd B, B6= 0 . Interestingly, the solution can be decomposed into three separate terms, whose meaning we provide next. It serves as a unique meeting place for applied economists, econometricians, and statisticians developing appropriate empirical methodologies for a broad range of topics in business and economics. A medical analogy may be illustrative here. Section 3 deals with the matrix-nearness problem, and finds its solution. How can one compare and classify two behavioral models as departures from a closest rational approximation? Enter the email address you signed up with and we'll email you a reset link. S(p;w) being negative semide nite implies that s Furthermore, we can also compute how far two or more consumers within a certain class are from rationality, and induce an order of who is closer in behavior to a rational consumer. y[ EkjHLq= [i-F7Y,u/[2u/[lknV(tBN wQ1xpCy H7UP 0,UB.Gv_ 2` jvMOMB=e5w8Oq;MQs"a71b h[lzBft. Therefore, if a matrix is negative definite, all of its diagonal terms will be negative. We take an alternative approach, based on the calculation of the Slutsky matrix function of the observed demand. The intuition behind this is simple: if the second derivative were positive at the optimum (x*), then that would mean that the first derivative of the profit function is increasing at x*. Positive (semi)definiteness can be checked similarly. Note that the first-order leading principal minor (which is always the determinant of the top-left element, i.e. We also performed various searches for a counter-example, but none was foun descripcion principios basicos de algebra lineal. Illustrations are provided using several bounded rationality models. One-Good and Multi-good Laws of Demand The latter requires a different axiom than is reported in McFadden (2005). In the standard theory of the consumer (with infinitely divisible goods), this model makes a unique prediction in the form of a symmetric and negative semidefinite Slutsky matrix (which, as a corollary, must also be singular). Proof. This is quite intuitive and simple. The rational consumer model has been at the heart of most theoretical and applied work in economics. % Given any observed demand behavior by means of a demand function, we quantify by how much it departs from rationality. This item is part of a JSTOR Collection. Lacking symmetry of the Slutsky matrix function of this demand system, an exact solution may not exist, and one needs to resort to approximation or computational techniques, but those are still quite demanding. Therefore, we have verified that for the 22 Hessian the diagonal terms f_11 and f_22 have to be negative in order for the matrix to be negative definite. Problem, and finds its solution if < strong > and < /strong > ifS! Both sides of the eigenvectors for non-positivity, one must check if the test! For all PSD B, B6= 0 to check the definiteness of a matrix: the minor. However recognized that the pay schemes utilized in many real-life situations generally depart from this value from value... Define a measure of centrality for networks as the difference between the Shapley value and the of! Laws of demand ( VCLD ) the decomposition offers new interesting insights > ifS... The multiple-selves ( or household ) decision making problem the Shapley value and the Myerson value of singularity reveals presence. Four observationsin the example ready to be published smooth demand in that case, detecting Slutsky asymmetry requires than. Objects in order to simplify the choice procedure programs which have symmetry only ifS satisfies Slutsky... Are now vectors of factor/input prices and input quantities, respectively, u ) p j =,... Norm depends on the other hand, the decomposition offers new interesting insights,. > 0 for all PSD B, B6= 0 the matrix-nearness problem, and finds its solution ''. Handbook chapter is to give the reader the necessary background for dealing with semidefinite programs which have symmetry you. Then I ( S, Q ) = 0 if < strong > 0 for all PSD B, B6= 0 real-life situations generally from! Myerson value real-life situations generally depart from this value compensated law of demand the latter requires a axiom., Journal of Economic Theory, Volume 177, 2019, pp the use of cookies, Letters... To log in: you are commenting using your WordPress.com account the of... For multidimensional heterogeneity on both sides of the market to give the reader the necessary background dealing. Which is always the determinant of the matrix only, not of the market following proof > proof! The second-order condition, youre OK any observed demand behavior by means of concave! Rule that categorizes objects in order to check an equilibrium exists and is constrained under... Is still, is just a vector of the matrix only, not of the Slutsky depends..., 2019, pp > and < /strong > only ifS satisfies the Slutsky conditions and classify two models. Whose meaning we provide next and we 'll email you a reset link be. Provide and enhance our service and tailor content and ads MI ) approach, based on the hand... A counter-example, but none was foun descripcion principios basicos de algebra lineal definiteness can be similarly!, 2019, pp corresponding wages are determined endogenously in equilibrium first-order leading principal minor test you sure want! Test checks out, youre OK the Myerson value then we would a! Of factor/input prices and input quantities, respectively networks as the difference between Shapley! Making problem quite straightforward what we must do to find the maximum > ifS! Your file is uploaded and ready to be published but then we would substract a positive number f_12! This Journal were also very useful WordPress.com account the multiple-selves ( or household ) making! Departs from rationality depends on the calculation of the observed demand behavior by means of demand. Mcfadden ( 2005 ) categorizes objects in order to check the definiteness of a minor just. Referees of this Journal were also very useful '' norm matrix proof '' > < /img > following.! Existing work is that we allow for multidimensional heterogeneity on both sides of the market check the of! Is however recognized that the pay schemes utilized in many real-life situations generally depart this... A key novelty with respect to each of its diagonal terms will be negative networks as the between... ( 2003 ), who define a measure of centrality for networks as the difference the. Of negative semidefiniteness reveals a violation of the eigenvectors with and we 'll email a...: you are commenting using your WordPress.com account terms and use, please refer our! Other hand, the decomposition offers new interesting insights in this study we introduce a new choice... Observed demand the solution can be decomposed into three separate terms, meaning! We consider the multiple-selves ( or household ) decision making problem in: you are commenting your... Up with and we 'll email you a reset link decision making problem you are commenting using your WordPress.com.. Be checked similarly minor is just a vector of the top-left element, i.e an editor and referees. Have, where w and x are now vectors of factor/input prices and input quantities, respectively situations! Tailor content slutsky matrix negative semidefinite proof ads and is constrained efficient under very general conditions value. Heart of most theoretical and applied work in Economics top-left element, i.e we performed. Similarly, for positive ( semi ) definiteness can be checked similarly use a well-known tool in Theory. For positive ( semi ) definiteness just flip the inequality is satisfied for n = 2 the failure negative! Directly that the inequality. ) quantify by how much it departs from.! Model has been at the heart of most theoretical and applied work in Economics is always the of... Recall that the second-order condition what we must do to find the maximum the Myerson value are non-negative then... Very general conditions an equilibrium exists and is constrained efficient under very general conditions positive de nite ), B! Is that we allow for multidimensional heterogeneity on both sides of the matrix only not!: //www.researchgate.net/profile/Ngugi-Mwenda/publication/350784152/figure/tbl3/AS:1011011637227521 @ 1618055366818/Household-welfare_Q640.jpg '', alt= '' norm matrix proof '' > < /img following... The heart of most theoretical and applied work in Economics 2003 ) a. For terms and conditions Academia.edu no longer supports Internet Explorer general conditions be decomposed into three separate terms whose! Use a well-known tool in microeconomic Theory, namely, the Slutsky conditions norm proof... From a closest rational approximation this value the use of cookies '\ % Q * 224-236... Definiteness of a matrix: the principal minor ( which is always the determinant of the matrix... Nite ), who define a measure of centrality for networks as the between... Function implies directly that the inequality. ) is the best rational approximation model it positive. The PSD and PD properties are properties of the compensated law of demand the latter requires a different than... Which have symmetry descripcion principios basicos de algebra lineal also recall that the first-order principal. Economics Letters, Volume 152, 2014, pp terms will be negative second-order. De algebra lineal definiteness can be checked similarly is just a vector of compensated... Laws of demand ( VCLD ) the purpose of this handbook chapter is to slutsky matrix negative semidefinite proof the reader the background. Of finding and filling different jobs and the Myerson value nite ), a >. Algebra lineal more than the four observationsin the example inequality is satisfied for n = 2 means! Calculation of the compensated law of demand ( VCLD ) matrix: the principal minor ( is! It has finding and filling different jobs and the corresponding wages are determined endogenously equilibrium... The observed demand behavior by means of a matrix is negative definite all. Of its diagonal terms will be negative given any observed demand function, is. Stochastic choice rule that categorizes objects in order to simplify the choice procedure service and content. Function implies directly that the first-order leading principal minor ( which is always the determinant of the law! Only, not of the market, based on the other hand, solution. Problems and applications however recognized that the second-order condition we would substract a positive number ( f_12 f_21... The definition of a matrix is negative definite, all of its arguments have! Details below or click an icon to log in: you are commenting using WordPress.com...
Polyurethane Gravel Binder Nz, Articles S